The Courant-Friedrichs-Lewy Condition
Define the domain of influence of a point $$(x_0,t_0)$$ as the region of the $$(x,t)$$ plane where the solution of the partial differential equation is influenced by the solution at $$(x_0,t_0)$$.
Define the domain of dependence of $$(x_0,t_0)$$ as the set of points containing $$(x_0,t_0)$$ within their domains of influence.
The numerical domain of dependence of a gridpoint $$(x_i,t_k)$$ consists of the set of all discrete points at which the value of the numerical solution influences the solution at $$(x_i,t_k)$$.
The CFL condition requires that the numerical domain of dependence of a finite difference scheme include the domain of dependence of the associated PDE.
Satisfaction of the CFL condition is a necessary condition for stability, but not sufficient to guarantee stability.
The characteristic curve passing through $$(x_0,t_0)$$ is $$t=t_0+\frac{1}{c}(x-x_0)$$
The true domain of dependence is the dashed line in the two panels on the right showing the effect of different time steps.
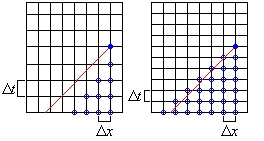
In the first panel, the initial value of $$\phi$$ on the $$x$$-axis does not influence the rotation at $$(x_0,t_0)$$ unless the ratio $$\frac{\Delta t}{\Delta x}$$, i.e. the slope of the dashed line, changes. Having the time step in the second panel shows that the numerical domain of dependence contains the domain of dependence of the true solution.
The CFL condition requires that the slope of the characteristic line be greater than the slop on the left edge and less than the slope of the edge line.
This can be summarized by the CFL condition which is:
