Computing the 1D Advection Equation
For the most part, analytical solutions of the linear advection equation are possible. However, real life problems deal with equations such as
\frac{\partial u}{\partial t} + \frac{\partial}{\partial x}(cu) = 0
where $$c$$ varies as a function of $$x$$ and so on.
We are interested in a numerical solution over the domain $$x_a \leq x \leq x_b$$ and $$t_s \leq t \leq t_e$$
Without loss of generality $$x_a=0, t_s=0$$
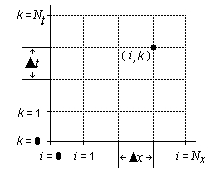
The domain is discretized as:
\require{AMSmath}
\begin{align*}
x_i & = x_a + \left(x_b-x_a\right)\frac{i}{N_x} & i = 0,...,N_x \\
t_k & = t_s + \left(t_e-t_s\right)\frac{k}{N_t} & k = 0,...,N_t
\end{align*}
$$N_x$$ is the number of discrete points in $$x$$
$$N_t$$ is the number of discrete points in $$t$$
Let $$\Delta x=\frac{x_b-x_a}{N_x}$$ and $$\Delta t=\frac{t_e-t_s}{N_t}$$ be the space--and time--steps with discrete values given by $$\phi_i^k$$.
