Research Interests

Nowadays, very high-dimensional datasets are becoming increasingly available in fields like computational vision, speech, biology or the social sciences.  Model selection within these high-dimensional spaces is difficult, particularly when the number of observed samples is small.  Many modern challenges in statistical modeling and inference are formulated within these so-called “small n, large d” scenarios, where asymptotic results are simply not applicable due to the lack of a sufficiently large set of observations. In the absence of any penalization, the sheer combinatorial complexity of the problem frequently leads to model over-fitting.  Simply penalizing model complexity tends to bias estimation towards the absence of interactions, blocking the discovery of important relationships that may actually exist.  Within this context, I believe that the introduction of carefully chosen biases and the enforcement of strong modeling assumptions based on prior expert knowledge can be used to improve the generalization capabilities of learning algorithms.  My research, under the supervision of Professors Donald Geman and Laurent Younes, focuses on the development of new, reliable statistical learning techniques and families of models that allow us to achieve this goal.

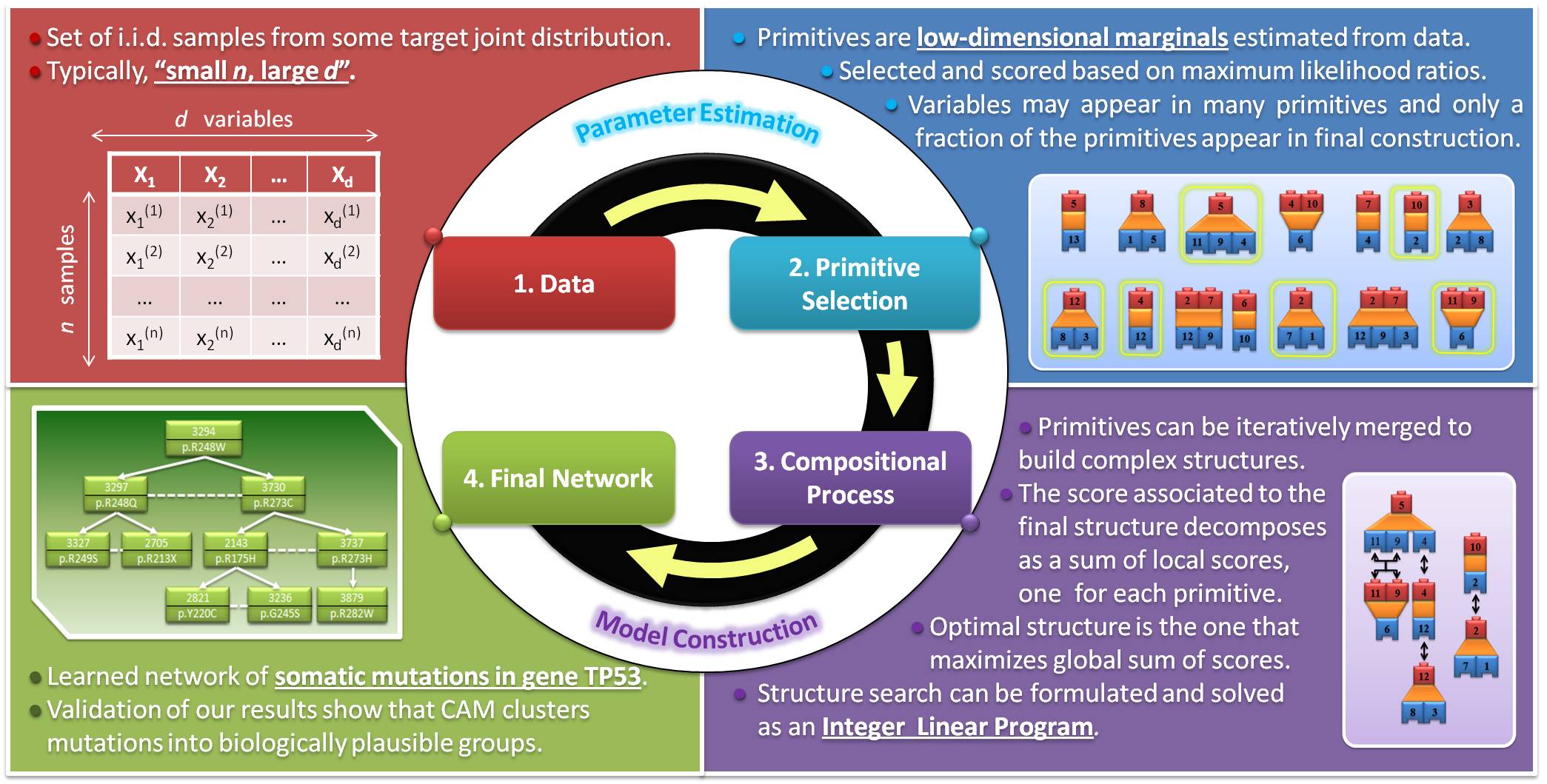
Competitive Assembly of Marginals

In my Ph.D. thesis, working together with my two advisors and Professor Jason Eisner from the Computer Science department, I have developed a new family of hierarchical, decomposable probabilistic graphical models that make it possible to efficiently capture relationships of statistical dependence in small-sample regimes.  The ultimate goal is to learn a good approximation of the multivariate probability distribution that describes the behavior of certain complex biological systems, namely molecular networks that model biochemical interactions within the cell.  This includes, but is not limited to, gene regulatory networks (where each node represents the level of expression of a certain gene inside a cell) and networks of statistical dependencies between mutations (where each node represents the presence or absence of a certain SNP in some DNA sample extracted from a patient).  We propose to follow a compositional approach where small subsets of elementary blocks corresponding to bivariate and trivariate discrete probabilities are first learned from data and then merged in a stepwise, lego-like manner in order to build high-dimensional distributions. We use the name CAM (which stands for Competitive Assembly of Marginals) to refer to these models.  Once the appropriate statistical framework has been introduced, the search for the best structure can be reformulated as an optimization problem that can be efficiently solved for reasonably large sets of variables.  Experimental results show that, for small sample sizes such as the ones encountered in many modern biomedical applications, these new models are competitive with the current state-of-the-art.

CAM overview

A video presentation from the IMA workshop on "Large Graphs: Modeling, Algorithms and Applications" where my advisor Don Geman gives a quick overview of CAM models can be found here.

Publications

Posters

Technical reports

Presentations

  • "A New Compositional Framework for Learning Multivariate Distributions from Small Samples", invited talk at the National Human Genome Research Institute in Rockville, MD (May 24, 2012).

  • "Measuring the Impact of a Random Variable". Student seminar at the Applied Mathematics and Statistics Department, Johns Hopkins University (March 9, 2010).

  • "Probabilistic Graphical Models for Small-sample Network Inference". Student seminar at the Institute for Computational Medicine, Johns Hopkins University (July 23, 2008).