Introduction to Metric Pattern Theory

Dedicated to Profress Ulf Grenander

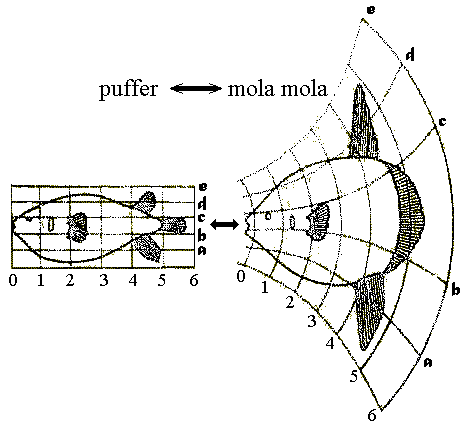
Revolutionary advances in the development of digital imaging modalities combined with advances in digital computation are enabling researchers to make major advances in the precise study of the awesome biological variability of human anatomy. This is emerging as the exciting new field of computational anatomy (CA) (Grenander and Miller, 1998). CA has three principal aspects: (i) automated construction of anatomical manifolds, points, curves, surfaces and subvolumes, (ii) comparison of these manifolds, and (iii) the statistical codification of the variability of anatomy via probability measures allowing for inference and hypothesis testing of disease state.

Although the study of structural variability of such manifolds can certainly be traced back to the beginnings of modern science, D'Arcy Thompson in his influential treatise `On Growth and Form' in 1917 had the clearest vision of what lay ahead, viz:

"In a very large part of morphology, our essential task lies in the comparison of related forms rather in the precise definition of each; and the deformation of a complicated figure may be a phenomenon easy of comprehension, though the figure itself may have to be left unanalyzed and undefined. This process of comparison, of recognizing in one form a definite permutation or deformation of another, apart altogether from a precise and adequate understanding of the original `type' or standard of comparison, lies within the immediate province of mathematics and finds its solution in the elementary use of a certain method of the mathematician. This method is the Method of Coordinates, on which is based the Theory of Transformations."

The study of shape and structure has certainly progressed a long way; Thompson's vision is precisely the mathematical structure we term anatomy in CA, a Grenander deformable template (Grenander, 1996) in which the space of anatomical imagery is an orbit under groups of transformations. There are two types of transformations, the first of the geometric or shape type studied through mappings of the coordinate systems of the anatomies. Variation in the image space is accomodated by introducing groups of diffeomorphic transformations carrying individual elements from one to another. The diffeomorphic transformations (invertible differentiable mappings with differentiable inverse) fill out the anatomy. Equally exciting is that in recent years metric space structures have been associated with the orbits of anatomical imagery. The metric is calculated via equations of motion describing the geodesic connection between the elements.

Thus the original vision of Grenander's Metric Pattern Theory (Grenander, 1994) is in large part being carried out in CA: metric distances between patterned shapes and structures are measured via distances between the mappings.

Chapters

1. Introduction to Group Theory
2. Introduction to Matrix Groups
3. Introduction to Group Actions & Orbits
4. Introduction to Lie Groups
5. Introduction to Deformable Templates
6. Introduction to Metric Mapping

Additional Chapters

1. Introduction to Dynamic Programming
2. Introduction to Curvature and the Shape Operator
3. Introduction to Numerical Solution of the 1D Linear Advection Equation

Sources

• Grenander, U, and Miller, MI, "Computational Anatomy: An Emerging Discipline," Quarterly of Applied Mathematics, LVI, No. 4,617-694, December, 1998.
• Grenander, U. 1996. Elements of Pattern Thoery. The Johns Hopkins University Press, Baltimore, MD.
• Grenander, U. 1993. General Pattern Theory: A Mathematical Study of Regular Structures. Oxford University Press Inc., New York, NY.
• Thompson, D'Arcy Wentworth. 1917. On Growth and Form..Cambridge University Press, England.
• Singer, SF. 2001. Symmetry in Mechanics: A Gentle, Modern Introduction. Birkhauser, Boston, MA.

Web adaptation (XHTML + CSS + SVG + JS) by Shane Steinert-Threlkeld of Mathwright Microworlds originally done by Faisal Beg, Kate Johnson, Mark Mattson, Priyan Weerappuli, and Dr. J T Ratnanather. This adaptation is part of "Interactive Introduction to Computational Medicine" technology fellowship granted by JHU Center for Educational Resources.