Problem 4: Shortest Path 3
This problem is identical to the last problem except in that there are two additional paths that have been included in the traverse. Find the shortest path from A to K in this course where there are now 5 paths to choose from instead of the 3 available in the previous example.
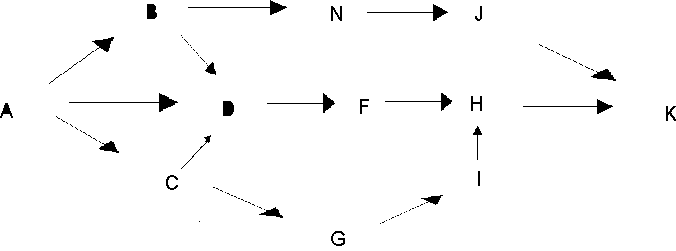AC
AB
AD
BN
NJ
JK
DF
FH
HK
CG
GI
IH
BD
CD
Problem 3: Shortest Path 2
Stage 5:
Stage 4:
Stage 3:
Stage 2:
Stage 1:
Your traverse distance is:
Compare your answer to the total lengths of the other courses to see if you've found the shortest path!
A-B-N-J-K:
A-D-F-H-K:
A-C-G-I-H-K:
A-C-D-F-H-K:
A-B-D-F-H-K:
