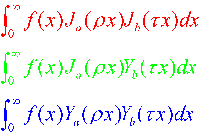A problem in auditory physiology requires computing infinite integrals involving products of two Bessel functions of the first or second kind. Such integrals occur in fluid dynamics, elasticity, electrodynamics and biophysics to name but a few applications. We have developed and tested a MATLAB toolbox called IIPBF. It was used to compute kernels in a system of Fredholm Integral equation of the second kind that arose in models of a viscous fluid jet impinging on an infinite plane (Davis et al. 2012; Davis et al. 2013).
The zipped file is located at the ACM TOMS website. Alternatively it can be downloaded from here. It also contains comparisons with more than 30 test integrals and with an alternative toolbox BESSELINT.
The toolbox can be applied to Bessel functions with non-integer order and complex-valued kernels that can arise in imaging applications.
Also available is a modification for just one Bessel function.
Improvements (including faster computations) can be found in these papers
- Michalski and Mosig (2016) Efficient computation of Sommerfeld integral tails – methods and algorithms
- Ledder and Zlotnik (2017) Evaluation of oscillatory integrals for analytical groundwater flow and mass transport model
- Suguira and Hasegawa (2021) Quadrature rule for indefinite integral of algebraic–logarithmic singular integrands
- Hasegawa and Suguira (2024) An automatic quadrature method for semi-infinite integrals of exponentially decaying functions and its Matlab code
- Lombardi and Papapicco (2024) Quadrature of functions with endpoint singular and generalised polynomial behaviour in computational physics
- Lovat and Celozzi (2024) Rapidly convergent series and closed-form expressions for a class of integrals involving products of spherical Bessel functions
